Formelsammlung
Rolfs Formelsammlung mit Java-Applet
um Zahlenbeispiele zu rechnen.
(mit den meisten neueren Browsern funktioniert Java leider nicht mehr)
Physik
Chemie
Astronomie
Mathematik
Anmerkungen:
- Da das Wurzelzeichen in HTML nicht immer korrekt dargestellt werden kann,
wird zum Teil noch sqrt() verwendet.
- Statt ex wird manchmal exp(x) geschrieben.
- Da seit der Neudefinition der Loschmidtschen Zahl (1986) nicht mehr klar
ist ob jetzt Teilchen pro Molvolumen oder Teilchen pro Milliliter gemeint
sind, wird jetzt nur noch die Bezeichnung Avogadrozahl benutzt. Ist exakt
das gleiche wie früher die Loschmidtsche Zahl, nämlich Anzahl
Teilchen pro Mol.
Rechnen mit Einheiten ,
magische Zahlen ,
Griechische Buchstaben
Stichwort-Suche , neue Formeln , Fehlerreport
Physik
Geschwindigkeit
ds=zurückgelegte Strecke dt=gebrauchte Zeit v=Geschwindigkeit
dv=Geschwindigkeitsänderung in der Zeit dt a=Beschleunigung
Beschleunigungskraft
a = Beschleunigung m = beschleunigte Masse
m = Masse v = Geschwindigkeit r = Rotationsradius
Zahlenbeispiel
m1, m2 = Massen
v1, v2 = Geschwindigkeiten vor dem Stoss
w1, w2 = Geschwindigkeiten nach dem Stoss
alle Geschwindigkeiten mit Vorzeichen
Einaches Beispielprogramm (c++ ubuntu): elastischerstoss.tar.gz
Gravitation (Schwerkraft)
siehe Astronomie->Gravitation
R = 1 + (1/2)2 · sin2(a/2) + (1/2 · 3/4)2 · sin4(a/2) + ...
R = Korrekturfaktur für grosse Pendelauslenkung
a = Winkel der Maximalauslenkung
L = Pendellänge (Aufhängung bis Schwerpunkt)
g = Erdbeschleunigung
| E = F·s | | F=Kraft, s=zurückgelegter Weg (Beispiel: Hubarbeit) |
| E = m·v²/2 | | m=Masse, v=Geschwindigkeit |
| E = m·c² | | c=Lichtgeschwindigkeit, m=Masse (z.B. bei Kernreaktion umgesetzte Masse) |
| E = h·ν | | Plancksche Formel |
| E = U·I·dt | | in der Elektronik |
Zahlenbeispiele
dE=umgesetzte Energie
dt=Zeitdauer
Ohmsches Gesetz, Leistung, Energie
| U = R·I | | Ohmsches Gesetz |
| P = U·I | | Leistung |
| E = P·t | | Energie |
U=Spannung (Volt)
R=Widerstand (Ohm 1Ω=1V/1A)
I=Strom (Ampere)
P=Leistung (Watt 1W=1V*1A)
t=Zeit (Stunden h, oder Sekunden s)
E=Energie (Wattstunden 1Wh=1W*1h, oder Joule 1J=1W*1s)
Zahlenbeispiele
Strommenge und Kapazität
| Q = I·t | | Strommenge |
| C = Q/U | | Kapazität |
Q=Strommenge (Coulomb: 1C=1As)
C=Capazität (Farad: 1F=1As/V=1C/V)
t=Zeit (in Sekunden)
Ein Coulomb ist die Strommenge wenn 1 Ampere 1 Sekunde lang fliesst.
Ein Kondensator hat eine Kapazität von 1 Farad wenn er
eine Strommenge von 1 Coulomb pro Volt speichern kann.
Es ist etwas verwirrend, dass das Formelzeichen für Kapazität
das gleiche Symbol (C) hat wie die Einheit der Strommenge (Coulomb).
Eine weitere Verwirrung ergibt sich weil das Formelzeichen der
Faraday-Konstanten das gleiche Symbol (F) hat
wie die Einheit der Kapazität (Farad).
Elektrolyse
n=Stoffmenge (in mol)
k=Anzahl benötigte Elektronen pro Molekül
F=Faraday-Konstante (96485 As/mol = 26.802 Ah/mol)
Die Elektrolytische Umsetzung von n Mol einer Substanz braucht also
eine Strommenge von Q Amperesekunden.
Beispiel: Wenn 10 mMol Nitrobenzol mit 1A reduziert werden sollen
braucht man 0.01*4*26.8 = 1.07 Stunden.
Wechselstrom
P=Wirkleistung
Q=Blindleistung
S=U·I=Scheinleistung
φ=phi=Phasenverschiebung zwischen Spannung und Strom
cos(φ)=P/S (=Wirkungsgrad?)
| h = | Höhe ueber Referenzpunkt |
| p = | aktueller Druck bei Höhe h |
| p0 = |
aktueller Druck bei Referenzpunkt (z.B. Meereshöhe) |
| T = | Temperatur in Grad Kelvin |
| k = | Konstante nach folgender Formel: |
| T0 = | Normaltemperatur (273 K) |
| p00 = | Normaldruck (1013mbar) (durchschnittlicher Druck auf Meereshöhe) |
| r0 = | Dichte der Luft bei T0 und p00 |
| g = | Erdbeschleunigung (9.80665 m/s²) |
| Zahlenbeispiel |
| Herleitung der Formel |
Lorentztransformation
Wenn zwei Koordinatensysteme K(x,y,z) und K'(x',y',z') sich gegeneinander
mit der Geschwindigkeit v entlang der x-Achse bewegen gilt:
t = Zeit gemessen in K
t' = Zeit gemessen in K'
c = Lichtgeschwindigkeit
Energie einer schnell bewegten Masse
Addition von Geschwindigkeiten
Wenn beide Geschwindigkeiten viel kleiner als Lichtgeschwindigkeit,
wird daraus in guter Näherung v=v1+v2.
h = Plancksche Konstante (Wirkungsquantum)
ν = Frequenz (Anzahl Wellen pro Sekunde)
λ = Wellenlänge
c = Lichtgeschwindigkeit
E = Energie eines Photons (Lichtquants)
Zahlenwertgleichung: E = 0.002857·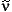
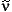 | = Wellenzahl in cm-1 (Anzahl Wellen pro Zentimeter) |
| E | = Energie in kcal/mol |
| Zahlenbeispiele |
k = Boltzmann-Konstante
T = Temperatur in Grad Kelvin
h, ν, c gleiche Bedeutungen wie in Plancksche Formel
Zahlenbeispiel
| n = | Brechungsindex |
| α = | Einfallswinkel zwischen Lot und Strahl |
| β = | Ausfallswinkel zwischen Lot und Strahl |
| c1 = | Lichtgeschwindigkeit im ersten Medium |
| c2 = | Lichtgeschwindigkeit im zweiten Medium |
| | Zahlenbeispiele |
| c = Konzentration in mol/l |
| d = Schichtdicke in cm |
| ε = Extinktionskoeffizient in l/(mol*cm) |
| I = Intensität nach der Probe |
| I0 = Intensität vor der Probe |
Umrechnung von Druck in Konzentration
| |
c = 0.0160·P/T |
Zahlenwertgleichung für ein ideales Gas |
c = Konzentration in mol/l
P = Druck in Torr
T = Temperatur in Grad Kelvin
Zahlenbeispiele
Absorptionsquerschnitt (Absorption Cross Section)
c = Konzentration in Moleküle/cm³
d = Schichtdicke in cm
σ = Absorptionsquerschnitt in cm²/Molekül
Umrechnung von Extinktionskoeffizient in Absorptionsquerschnitt
Optisch aktive Moleküle können linear polarisiertes Licht drehen.
Der Drehwinkel ist proportional zur Konzentration und Schichtdicke.
| α | = | gemessener Winkel |
| L | = | Schichtdicke in dm |
| c | = | Konzentration in g/ml |
| αD | = | Drehwinkel auf Schichtdicke 1dm und Konzentration 1g/ml normiert |
| D | = | Natrium-D Linie = 589nm |
| | | (α ist stark Wellenlängenabhängig, sogar das Vorzeichen kann wechseln!) |
| | | (da es auch noch Temperaturabhängig ist, wird diese meist auch mit angegeben [α]tD ) |
Berechnung der Frequenz einer Streckschwingung. Diese Formel gilt eigentlich
nur für zweiatomige Moleküle, aber kann auch als Näherungsformel
in grösseren Molekülen verwendet werden.
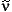 | = | Frequenz in Wellenzahlen |
| K | = | Kraft zwischen den beiden beteiligten Atomen in mdyn/Angström |
| | | (kann mit etwa 5.5 mdyn/Angström pro Bindung geschätzt werden) |
| m1 | = | Masse des ersten Atoms |
| m2 | = | Masse des zweiten Atoms |
Verschiebung der Frequenz einer Streckschwingung beim Einsetzen eines Isotops:
Zahlenbeispiele
Reduzierte Masse: Damit werden obige Formeln etwas einfacher:
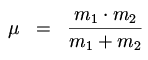
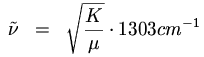
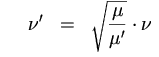
Dies ist eine Empirische Formel zur Darstellung der Beziehung zwischen
Dihedralwinkel (auch Diederwinkel genannt)
und 3J-Aufspaltung im NMR-Spektrum.
Originalformel von Karplus:
Neuere Variante1:
Neuere Variante2:
Bei verschiedenen Atomen oder unterschiedlicher chemischer Umgebung werden
unterschiedliche Parameter verwendet.
Die beiden Formelvarianten werden oft verwechselt.
Parametersätze die im Internet zu finden sind,
können also zu der einen oder andern Formel gehören.
Manchmal sind auch noch A und C vertauscht.
Umrechnung der Parameter:
Einige Parametersätze:
| Atome |
A1 |
B1 |
C1 |
| HCCH | -0.28 | -0.5 | 9.0 |
| HNCH | 1.9 | -1.4 | 6.4 |
| HNCH | 2.5 | -1.2 | 6.8 |
Zahlenbeispiele
| C | = Konzentration in mol/l |
| CTMS | = TMS-Konzentration in mol/l |
| ITMS | = Integral des TMS-Peaks |
| IH | = Integralwert für ein H |
Wenn die TMS-Konzentration gleich 1 Volumenprozent ist:
Wenn wir eine Flüssigkeit durch eine Kapillare laufen lassen gilt:
η = Viskosität
D = Dichte der Flüssigkeit
G = Gerätekonstante (Dicke, Länge der Kapillare, durchgeflossene Menge)
t = Durchflusszeit
Das mittlere Molekulargewicht eines gelösten Polymers ist:
| η | = | Viskosität der Lösung |
| η0 | = | Viskosität des reinen Lösungsmittels |
| t | = | Durchflusszeit der Lösung |
| t0 | = | Durchflusszeit des reinen Lösungsmittels |
| c | = | Konzentration in g/ml |
| w | = | reduzierte spezifische Viskosität = ηsp/c |
| w0 | = | Approximierter Wert von w bei c=0 |
| | (Andere Bezeichnungen: [η], Staudingerindex, Grenzviskosität, intrinsic viscosity) |
| K | = | Konstante die von Molekül und Lösungsmittel abhängig ist |
| a | = | weitere von Molekül und Lösungsmittel abhängige Konstante |
Der zweite Teil der w-Gleichung ist eine Näherung und stimmt nur wenn
die Dichte der Lösung nicht stark von der Dichte des reinen
Lösungsmittels abweicht (also für kleine Konzentrationen).
Um w0 zu erhalten werden mehrere Messung bei verschiedenen
Konzentrationen gemacht, w gegen c aufgetragen, und mit einer
Ausgleichsgeraden der Wert bei c=0 ermittelt.
Die empirisch bestimmten Werte a und K sind zum Teil in Tabellen zu finden.
a liegt meist zwischen 0.5 und 2.0.
Beispiele:
| Substanz | Lösungsmittel | K | a |
|---|
| Polystyrol | CHCl3 | 0.0112 | 0.73 |
| PBLG | DCA | 2.78e-3 | 0.87 |
| PBLG | DCA | 1.747e-3 | 0.886 | (eigne Messung) |
| Polyalanin | DCA | 0.364 | 0.672 |
p = Druck in Pascal
T = Temperatur in Kelvin
V = Volumen in m³ (1 Kubikmeter = 1000 Liter)
n = Molzahl (= Anzahl Teilchen / NA)
R = Gaskonstante = 8.315 J/mol/K
(Wenn p in mbar und V in Liter: R=83.15 mbar*l/mol/K)
Zahlenbeispiele
Kann auch als p*V=N*k*T geschrieben werden. (mit N=Anzahl Teilchen, und
k=Boltzmann-Konstante)
Geschwindigkeitsverteilung
Die Geschwindigkeitsverteilung der Moleküle (Atome bei Edelgas)
in einem idealen Gas ist:
k1 = 4Pi*(M/(2PiRT))1.5
k2 = M/(2RT)
M = Molmasse in kg/mol
R = Gaskonstante in J/mol/K
T = Temperatur in K
Dabei ist s die Geschwindigkeit in m/s. Die Funktion f(s) ist so definiert,
dass die Wahrscheinlichkeit dass ein Teilchen eine Geschwindigkeit zwischen
s und s+ds hat, gleich f(s)*ds ist.

Der Mittelwert (quadratisches Mittel) der Teilchengeschwindigkeiten ist:
Temperaturskalen
0 K = absoluter Nullpunkt (Moleküle bewegen sich nicht mehr),
273.16 K = Temperatur beim Tripelpunkt von Wasser.
Beim Tripelpunkt stehen Feste-, Flüssige- und Gasförmige-Phase eines
reinen Stoffs im Gleichgewicht. Beim Wasser ist das dann eben bei
0.01oC und etwa 6.107mbar der Fall. (Man beachte dass das für
einen _reinen_ Stoffs gilt, die Luft muss man also abpumpen um den Tripelpunkt
zu messen.)
Celsius:
Ursprüngliche Definition: 0oC = Schmelzpunkt, 100oC = Siedepunkt von Wasser bei Normaldruck (1bar).
Neue Definition: 0oC = 273.15 K, Differenzen in Celsius = Differenzen in Kelvin
(da der Tripelpunkt von Wasser als 273.16 definiert wurde ist der Schmelzpunkt
von Wasser bei 1bar immer noch ziemlich genau bei 0oC)
Farenheit:
Ursprüngliche Definition: 100oF = Körpertemperatur,
0oF = Temperatur der Ammonium-Wasser-Eis Kältemischung
F = C*9/5+32
C = (F-32)*5/9
Zahlenbeispiele Temperatur-Umrechnungen
Wärmemenge
Q = Wärmemenge (Energiemenge)
dQ = Änderung der Wärmemenge bei Änderung der Temperatur um dT
(dabei sollte dT so klein sein dass sich k nicht ändert)
k = Wärmekapazität (Energiemenge um 1 Gramm um 1 Kelvin zu erwärmen)
(ist stark Stoffabhängig und wenig Temperaturabhängig)
m = Masse (in Gramm)
Zahlenbeispiel:
die Wärmekapazität von Wasser ist 4.1868 Joule/g.
Wieviel Energie braucht man um 1l Wasser von 20o auf
100oC zu erwärmen?
(k für Wasser ist eigentlich bei 4oC, stimmt aber auch
zwischen 0 und 100o ziemlich gut)
Entropie
dS = dQ/T
S=Entropie
Q=Wärmemenge
Wärmekapazität von idealem Gas

Bei Gasen gibt es zwei verschiedene Wärmekapazitäten.
Bei konstantem Volumen wird die molare Wärmekapazität cv genannt,
bei konstantem Druck hingegen ist es cp.
Dabei ist cp grösser, da noch die mechanische Energie
P*dV dazukommt.
Für Edelgase gilt:
cv = 3/2 * R
cp = cv + R
Einheit ist jeweils J/mol/K
Obige Formeln lassen sich leicht aus dem Gasgesetz herleiten.
Formel für nicht ideale Gase:
f = Freiheitsgrad, 3 für Edelgase, 5 oder mehr für alle andern
Der Freiheitsgrad ist stark Stoff- und Temperatur-abhängig.
Adiabatische Kompression eines Gases
Mit adiabatisch ist gemeint, dass es keinen Wärmeaustausch (Energieaustausch) zwischen
dem Gas und der Umgebung gibt. Das ist natürlich eine idealisierte Vorstellung, da in
der Realität ein Wärmeaustausch nicht vollständig verhindert werden kann.
k = Isentropenexponent (Kappa)
f = 2/(k-1) = Freiheitsgrade, f=3 bei einatomigem Gas, f=5 bei 2-atomigem Gas (z.B. N2)
Bei Edelgasen (ideales Gas) ist f=3 und k-1 ist somit 2/3
Zahlenbeispiel:
Wenn Stickstoff von Raumtemperatur um einen Faktor 10 komprimiert wird, wie warm wird er dann?
Chemie
Das Molekulargewicht eines Moleküls wird berechnet indem einfach die
Werte der einzelnen Atome addiert werden.
Tips:
Gross/Klein-Schreibung ist wichtig!
Peptide können auch eingegeben werden.
Ohne Schutzgruppe am Anfang muss ein H- mitangegeben werden, ohne Schutzgruppe
am Ende brauchts ein -OH. (z.B. H-Ala-OH)
Beispiel: Boc-Ala-Gly-OH sollte 246.263 (246.121) ergeben.
Hier noch eine kleine Dokumentation als Textdatei.
Man kann das Programm auch lokal (unter Linux oder auf Palm) installieren:
MG-Rechner
Ein Puffer ist eine wässrige Lösung, die versucht den pH-Wert konstant zu halten.
pH = negativer Logarithmus der Wasserstoffionenkonzentration (pH-Wert)
pKs = Säurekonstante
A- = Konzentration des basischen Anteils (in mol/l)
HA = Konzentration der Säure (in mol/l)
Beispiele: Acetatpuffer
Natriumacetat und Essigsäure in gleichen Mengen (Anzahl Mol) in Wasser gelöst ergibt einen Puffer
mit pH 4.76 (pKs ist 4.76 und A- ist gleich HA).
Die Dichte von einer D2O-H2O-Mischung ist:
Der Mol-Anteil von D2O in einer Mischung mit Dichte D ist:
N1 = Molanteil von D2O
N2 = Molanteil von H2O
M1 = Molmasse von D2O
M2 = Molmasse von H2O
D1 = Dichte von reinem D2O
D2 = Dichte von reinem H2O
V1 = M1/D1 = Molvolumen von D2O
V2 = M2/D2 = Molvolumen von H2O
Zahlenbeispiel
Es soll eine Lösung eines Salzes durch weitere Zugabe von Salz
auf eine bestimmte höhere Konzentration gebracht werden.
Dazu muss jeweils die Dichte der Lösung bei den betreffenden Konzentrationen bekannt sein.
(z.B. aus Dichtetabellen)
v0 = Anfangsvolumen in ml
c0 = Anfangskonzentration in g/ml
d0 = Anfangsdichte (g/ml)
D = Dichte der Ziellösung
C = Zielkonzentration in g/ml
x = zuzugebende Menge in Gramm
v = erhaltenes Volumen in ml
Zahlenbeispiel
Beispiel: Es soll aus 1ml Wasser eine 6M GdmCl-Lösung gemacht werden:
C = 0.573 g/ml, D = 1.14 g/ml, c0=0, d0=1
Example: to make from 1ml water a solution of 6M GdmCl use this parameters:
C = 0.573 g/ml, D = 1.14 g/ml, c0=0, d0=1
Astronomie
| A = |
Mittlerer Abstand des Planeten zur Sonne |
| T = | Umlaufzeit |
| m1 = | Masse der Sonne |
| m2 = | Masse des Planeten (kann im Sonnensystem vernachlässigt werden) |
| k = |
Konstante = G/(4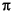 ²) ²) |
| |
im Sonnensystem kann man alle Unbekannten gleich 1 setzen, |
| |
also m1=1 Sonnenmasse, AE=1, TE=1 Jahr, |
| |
dann wird k=1 und wir können alle Planetendistanzen ausrechnen.
|
| Zahlenbeispiel |
JD = Anzahl Tage seit 4713 vor Christus
bis und mit 4.Oktober 1582: B = int((y+4716)/4) - 1181
ab 15.Oktober 1582: B = int(y/400)-int(y/100)+int(y/4)
(Wegen der Gregoranischen Kalenderreform folgte auf den 4.Okt. sogleich der 15.)
h = Tageszeit in Stunden
d = Tag
Y = für Jahre vor Christus: Y = -1 - Jahreszahl
für Jahre nach Christus: Y = Jahreszahl
wenn Monat<=2 : y = Y-1 m = Monat+13
sonst: y = Y m = Monat+1
int() = Abrundung auf ganze Zahl
Wer die Formel verstehen will sollte einige Beispiele von Hand ausrechnen.
Beispiel: 24.Dez. 1 vor Chr. um 20:15
h=20.25 d=24 Y=0 y=0 m=13 int(30.6*m)=397
Man kann die Formel aber natürlich auch verwenden ohne genau
zu verstehen wie sie funktioniert:
Zahlenbeispiele
Das "Julianische Datum" wird auch als "Julianischer Tag" bezeichnet (englisch "julian day").
Einige Leute halten diese Bezeichnung für treffender.
Mathematik
Zahlenbeispiel mit Java
Die Gausskurve (auch Glockenkurve genannt) kommt oft in
Wahrscheinlichkeitsrechnungen vor.
Als Normalverteilung (Gauss-Verteilung) wird die Formel auch so geschrieben:
| µ = | Erwartungswert |
 = = | Standardabweichung |
Eine Bezier-Kurve wird durch 4 Stützpunkte beschrieben.
Rekursive Definition:
Von den 4 Stützpunkten A B C D bilden A und D die beiden Endpunkte.
Man kann 2 kleinere Bezierkurven bilden:
A' = A
B' = (A+B)/2 also die Mitte zwischen A und B
C' = (A+2B+C)/4 Mitte zwischen B' und der Mitte von B und C
D' = (A+3B+3C+D)/8 Mitte zwischen C' und B''
und
A'' = D'
B'' = (B+2C+D)/4 Mitte zwischen C' und der Mitte von B und C
C'' = (C+D)/2 Mitte zwischen C und D
D'' = D
Die Menge aller A und D Punkte ergeben dann die Bezierkurve.
An der Uni-Oldenburg
wurden Bezier-Kurven einst ausführlich beschrieben. Leider nicht mehr
zu finden. Die dort angegebene Formel ist damit verloren gegangen.
Formeln zu Spline-Kurven sind hier zu finden:
B-Spline ,
B-Spline+andere
Aus Geographischen Koordinaten zweier Orte den Abstand berechnen.
Dies ist eine Näherungsformel (Erde wird als Kugel betrachtet).
Für genaue Werte sollte deshalb R je nach Geographischer Breite angepasst
werden.
| R = | Erdradius (6380km) |
| lata, lona = | Koordinaten des einen Punktes (Breite und Länge in Grad) |
| latb, lonb = | Koordinaten des zweiten Punktes |
| Zahlenbeispiel mit Java |
Zeit: s=Sekunde, min=Minute, h=Stunde
Strecke: m=Meter, km=Kilometer (k=Vorsilbe)
Geschwindigkeit: 1 m/s = 3.6 km/h
Beschleunigung: m/s2
Kraft: N = mkg/s2
Energie: J = Ws = m2kg/s2
| Energie-Einheit | Symbol | Wert in Joule |
|---|
| Wattsekunde | Ws | 1 |
| Kilokalorie | kcal | 4186.8 |
| Elektronenvolt | eV | 1.602*10-19 |
| Erg | Erg | 10-7 |
| Kilowattstunde | kWh | 3.6*106 |
Leistung: W = J/s = m2kg/s3
| Leistungs-Einheit | Symbol | Wert in Watt |
|---|
| Joule pro sekunde | J/s | 1 |
| Kilowatt | kW | 1000 |
| Pferdestärke | PS | 735.5 |
Druck: 1 mbar = 100 Pa = 100 N/m2
| Druck-Einheit | Symbol | Wert in mbar |
|---|
| Pascal | Pa | 0.01 |
| Torr | Torr | 1.3329 |
| PSI | PSI | 68.93 |
h = hekto = 100 ,
k = kilo = 1000 ,
M = Mega = 106 ,
G = Giga = 109 ,
T = Tera = 1012 ,
P = Peta = 1015 ,
E = Exa = 1018
d = dezi = 0.1 ,
c = centi = 0.01 ,
m = milli = 0.001 ,
µ = micro = 10-6 ,
n = nano = 10-9 ,
p = pico = 10-12 ,
f = femto = 10-15 ,
a = atto = 10-18
Boltzmann-Konstante k=R/NA=1.38066·10-23 J/K
Plancksches Wirkungsquantum h=6.626·10-34 m2kg/s
Lichtgeschwindigkeit c=299'792'458 m/s
Avogadro-Konstante NA=6.022142·1023 Teilchen/mol
(ist oft auch als "Loschmidtsche Zahl" oder NL anzutreffen)
Loschmidt-Zahl L = NA/v0 = 2.686777·1019 Teilchen/cm3
(neue Definition seit 1986 nach CODATA)
Gaskonstante R=8.31447 J/mol/K = 83.1447 mbar*l/mol/K
Molvolumen v0=22.414 l/mol
Erdbeschleunigung g=9.80665 m/s2
Gravitationskonstante G=6.67259·10-11
Absoluter Nullpunkt: -273.15oC = 0 K (Kelvin)
Elementarladung e=1.602176·10-19 C
Faraday-Konstante F=NA·e=96485.34 C/mol
Anhang
Avogadrozahl
Barometer , Beer ,
Beschleunigung ,
Brechung
Drehung ,
Optische Drehung
Einheiten , Energie
Farad , Faraday
Gasgesetz , Gausskurve ,
Gravitation
Isotop
Karplus
Lambert , Leistung ,
Loschmidt ,
Luftdruck
Normalverteilung
Pascal , Pendel ,
Planck
Refraktometrie
Schwarzkörperstrahlung ,
Schwerkraft ,
IR-Schwingung ,
Pendel-Schwingung
Temperatur
Viskosität
Watt
Wenn Sie einen Fehler in einer Formel entdeckt haben, senden Sie bitte eine
kurze e-mail.
Wenn Sie eine Formel kennen die hier hinein gehören würde, senden
Sie sie mir bitte über e-mail.
Wenn möglich als HTML-, LaTeX- oder Text-Datei. Wenn
möglich sollte eine Herleitung und/oder eine Quellenangabe dabei sein.
E-MAIL: rolf.pfister@chem.uzh.ch
Externe Links:
weitere Formelsammlungen ,
www.formel-sammlung.de
Zurück zu: Software ,
HTML-Ueberblick
 diese Seite wird noch laufend verbessert.
diese Seite wird noch laufend verbessert.


Last update: 12-Aug-2019 / 13-Mar-2025 / RPF
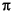 ·sqrt(L/g)·R
·sqrt(L/g)·R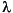
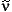
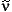
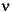 ) =
) =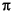 h
h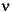 5
5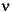 h/kT - 1
h/kT - 1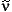 = √(K·(m1+m2)/(m1·m2)) · 1303cm-1
= √(K·(m1+m2)/(m1·m2)) · 1303cm-1
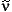
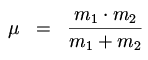
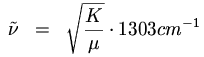
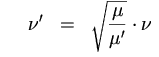
 - 0.28
- 0.28 <90o
<90o - 0.28
- 0.28 <180o
<180o + C1cos2
+ C1cos2
 + C2cos(2
+ C2cos(2 )
)


 ²)
²) ·sqrt(2π)
·sqrt(2π)
 2
2 =
= diese Seite wird noch laufend verbessert.
diese Seite wird noch laufend verbessert.